[코딩] Circle Square

클러스터링(Clustering)

 : 비지도 학습의 일종
 : 계층적 군집분석

 - 계층적 군집분석 종류

 - 응집형 : 자료 하나하나를 군집으로 간주하고, 가까운 군집끼리 연결하는 방법. 군집의 크기를 점점 늘려가는 알고리즘. 상향식

 - 분리형 : 전체 자료를 큰 군집으로 간주하고, 유의미한 부분을 분리해 나가는 방법. 군집의 크기를 점점 줄여가는 알고리즘. 하향식

k-means : 군집 수(k) 지정. 거리(유클리디안 거리 계산 법)들의 평균으로 비계층적 군집분석 진행.

 - 이론

m.blog.naver.com/PostView.nhn?blogId=gkenq&logNo=10188552802&proxyReferer=https:%2F%2Fwww.google.com%2F

 * cluster1.py

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
plt.rc('font', family='malgun gothic')

np.random.seed(123)
var = ['x', 'y']
labels = ['점0','점1', '점2', '점3', '점4']
x = np.random.random_sample([5, 2]) * 10
df = pd.DataFrame(x, columns = var, index = labels)
print(df)
'''           x         y
점0  6.964692  2.861393
점1  2.268515  5.513148
점2  7.194690  4.231065
점3  9.807642  6.848297
점4  4.809319  3.921175
'''

plt.scatter(x[:, 0], x[:, 1], c='blue', marker='o')
plt.grid(True)
plt.show()

from scipy.spatial.distance import pdist, squareform

dist_vec = pdist(df, metric='euclidean') # 데이터간 거리를 유클리디안 거리계산을 사용하여 측정
print('distmatrix :', dist_vec) 
# [5.3931329  1.38884785 4.89671004 2.40182631 5.09027885 7.6564396 2.99834352 3.69830057 2.40541571 5.79234641]

print(squareform(dist_vec)) # 데이터를 테이블 형태로 변경
'''
[[0.         5.3931329  1.38884785 4.89671004 2.40182631]
 [5.3931329  0.         5.09027885 7.6564396  2.99834352]
 [1.38884785 5.09027885 0.         3.69830057 2.40541571]
 [4.89671004 7.6564396  3.69830057 0.         5.79234641]
 [2.40182631 2.99834352 2.40541571 5.79234641 0.        ]]
'''

row_dist = pd.DataFrame(squareform(dist_vec))
print(row_dist)
'''
          0         1         2         3         4
0  0.000000  5.393133  1.388848  4.896710  2.401826
1  5.393133  0.000000  5.090279  7.656440  2.998344
2  1.388848  5.090279  0.000000  3.698301  2.405416
3  4.896710  7.656440  3.698301  0.000000  5.792346
4  2.401826  2.998344  2.405416  5.792346  0.000000
'''

from scipy.spatial.distance import pdist

distance=pdist(df, metric='euclidean') : 데이터간 거리를 유클리디안 거리계산을 사용하여 측정

from scipy.spatial.distance import squareform

squareform(distance) : 데이터를 테이블 형태로 변경

from scipy.cluster.hierarchy import linkage # 응집형 계층적 군집분석

row_clusters = linkage(dist_vec, method='ward') # method : complete, single, average, .. 
print(row_clusters)
'''
[[0.         2.         1.38884785 2.        ]
 [4.         5.         2.65710936 3.        ]
 [1.         6.         5.45400408 4.        ]
 [3.         7.         6.64710151 5.        ]]
'''

df = pd.DataFrame(row_clusters, columns=['클러스터1', '클러스터2', '거리', '멤버 수'])
print(df)
'''
   클러스터1  클러스터2        거리  멤버 수
0    0.0    2.0  1.388848   2.0
1    4.0    5.0  2.657109   3.0
2    1.0    6.0  5.454004   4.0
3    3.0    7.0  6.647102   5.0
'''

from scipy.cluster.hierarchy import linkage

linkage(distance, method='ward') :응집형 계층적 군집분석

method : complete, single, average, ... 

 - linkage API

docs.scipy.org/doc/scipy/reference/generated/scipy.cluster.hierarchy.linkage.html

from scipy.cluster.hierarchy import dendrogram

dendrogram(row_clusters, labels=labels)
plt.tight_layout()
plt.ylabel('유클리드 거리')
plt.show()

from scipy.cluster.hierarchy import dendrogram

dendrogram(linkage값, labels=) : dendrogram 생성

 - 계층적 클러스터 분류 결과 시각화

from sklearn.cluster import AgglomerativeClustering

ac = AgglomerativeClustering(n_clusters = 3, affinity='euclidean', linkage='ward')
labels = ac.fit_predict(x)
print('결과 :', labels) # 결과 : [0 2 0 1 0]

from sklearn.cluster import AgglomerativeClustering
AgglomerativeClustering(n_clueters = 3, affinty='euclidean', linkage='ward') : 병합 군집 알고리즘

a = labels.reshape(-1, 1)
print(a)
'''
[[0]
 [2]
 [0]
 [1]
 [0]]
'''
x1 = np.hstack([x, a])
print('x1 :', x1)
'''
x1 : 
[[6.96469186 2.86139335 0.        ]
 [2.26851454 5.51314769 2.        ]
 [7.1946897  4.2310646  0.        ]
 [9.80764198 6.84829739 1.        ]
 [4.80931901 3.92117518 0.        ]]
'''
x_0 = x1[x1[:, 2] == 0, :]
x_1 = x1[x1[:, 2] == 1, :]
x_2 = x1[x1[:, 2] == 2, :]

plt.scatter(x_0[:, 0], x_0[:, 1])
plt.scatter(x_1[:, 0], x_1[:, 1])
plt.scatter(x_2[:, 0], x_2[:, 1])
plt.legend(['cluster0', 'cluster1', 'cluster2'])
plt.show()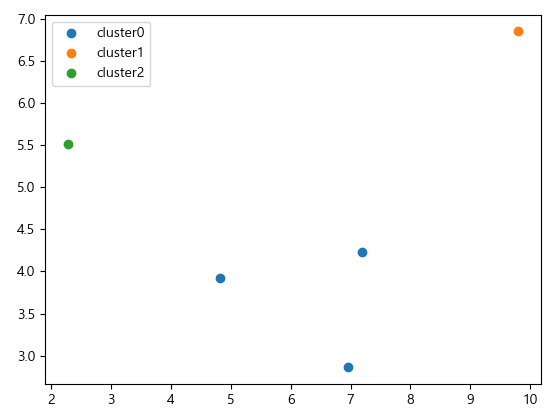

계층적 클러스터링 : iris

 * cluster2.py

import pandas as pd
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt

iris = load_iris()
iris_df = pd.DataFrame(iris.data, columns=iris.feature_names)
print(iris_df.head(3))
'''
   sepal length (cm)  sepal width (cm)  petal length (cm)  petal width (cm)
0                5.1               3.5                1.4               0.2
1                4.9               3.0                1.4               0.2
2                4.7               3.2                1.3               0.2
'''
print(iris_df.loc[0:4, ['sepal length (cm)', 'sepal width (cm)']])
'''
   sepal length (cm)  sepal width (cm)
0                5.1               3.5
1                4.9               3.0
2                4.7               3.2
3                4.6               3.1
4                5.0               3.6
'''

from scipy.spatial.distance import pdist, squareform

#dist_vec = pdist(iris_df.loc[:, ['sepal length (cm)', 'sepal width (cm)']], metric = 'euclidean')
dist_vec = pdist(iris_df.loc[0:4, ['sepal length (cm)', 'sepal width (cm)']], metric = 'euclidean')
print(dist_vec)   # 데이터간 거리
# [0.53851648 0.5        0.64031242 0.14142136 0.28284271 0.31622777
#  0.60827625 0.14142136 0.5        0.64031242]

row_dist = pd.DataFrame(squareform(dist_vec)) # 테이블 형태로 변경
print('row_dist :\n', row_dist)
'''
           0         1         2         3         4
0  0.000000  0.538516  0.500000  0.640312  0.141421
1  0.538516  0.000000  0.282843  0.316228  0.608276
2  0.500000  0.282843  0.000000  0.141421  0.500000
3  0.640312  0.316228  0.141421  0.000000  0.640312
4  0.141421  0.608276  0.500000  0.640312  0.000000
'''

from scipy.cluster.hierarchy import linkage, dendrogram
row_clusters = linkage(dist_vec, method='complete') # 응집형 계층적 군집 분석
print('row_clusters :\n', row_clusters)
'''
[[0.         4.         0.14142136 2.        ]
 [2.         3.         0.14142136 2.        ]
 [1.         6.         0.31622777 3.        ]
 [5.         7.         0.64031242 5.        ]]
'''

df = pd.DataFrame(row_clusters, columns=['id1', 'id2', 'dist', 'count'])
print(df)
'''
   id1  id2      dist  count
0  0.0  4.0  0.141421    2.0
1  2.0  3.0  0.141421    2.0
2  1.0  6.0  0.316228    3.0
3  5.0  7.0  0.640312    5.0
'''
row_dend = dendrogram(row_clusters)  # dendrodgram
plt.ylabel('dist test')
plt.show()

from sklearn.cluster import AgglomerativeClustering

ac = AgglomerativeClustering(n_clusters = 2, affinity='euclidean', linkage='complete')
x = iris_df.loc[0:4, ['sepal length (cm)', 'sepal width (cm)']]
labels = ac.fit_predict(x)
print('클러스터 결과 :', labels) # 결과 : [1 0 0 0 1]

plt.hist(labels)
plt.grid(True)
plt.show()

비계층적 군집분석

yganalyst.github.io/ml/ML_clustering/

21. 군집분석(Clustering) : 비지도학습 - 유클리디안 거리 계산법 사용

x <- matrix(1:16, nrow = 4)
x
# [,1] [,2] [,3] [,4]
# [1,]    1    5    9   13
# [2,]    2    6   10   14
# [3,]    3    7   11   15
# [4,]    4    8   12   16
help(dist)
d <- dist(x, method = "euclidean")
d
#   1 2 3
# 2 2    
# 3 4 2  
# 4 6 4 2
plot(d)
text(d, c(LETTERS[1:6]))

txt1 <- read.csv("testdata/cluster_ex.csv")
txt1
# irum kor eng
# 1 홍길동  80  90
# 2 이기자  70  40
# 3 유별나  65  75
# 4 강나루  85  65
# 5 전속력  95  87
plot(txt1[, c(2:3)],
     xlab ='국어',
     ylab ='영어',
     xlim = c(30, 100),
     ylim = c(30, 100),
     main = '학생점수')

text(txt1[, 2], txt1[, 3], labels = abbreviate(rownames(txt1)), cex = 0.8, pos = 1, col = "blue")
text(txt1[, 2], txt1[, 3], labels = txt1[,1], cex = 0.8, pos = 2, col = "red")

dist_m <- dist(txt1[c(1:2), c(2:3)], method = "manhattan")
dist_m
# 1
# 2 60

dist_e <- dist(txt1[c(1:2), c(2:3)], method = "euclidean")
dist_e
# 1
# 2 50.9902

 - 계층적 군집분석

x <- c(1,2,2,4,5)
y <- c(1,1,4,3,5)
xy <- data.frame(cbind(x,y))
plot(xy,
     xlab ='x',
     ylab ='y',
     xlim = c(0, 6),
     ylim = c(0, 6),
     main = '응집적 군집분석')

text(xy[, 1], xy[, 2], labels = abbreviate(rownames(xy)),
     cex = 0.8, pos = 1, col = "blue")
abline(v=c(3), col = 'gray', lty=2)
abline(h=c(3), col = 'gray', lty=2)

 - 유클리디안 거리 계산법

dist(xy, method = 'euclidean') ^ 2
#    1  2  3  4
# 2  1         
# 3 10  9      
# 4 13  8  5   
# 5 32 25 10  5

 - Dendrogram으로 출력

hc_sl <- hclust(dist(xy) ^ 2, method = "single") # 최단거리법
hc_sl
plot(hc_sl, hang = -1)

hc_co <- hclust(dist(xy) ^ 2, method = "complete") # 완전(최장) 거리법
hc_co
plot(hc_co, hang = -1)

hc_av <- hclust(dist(xy) ^ 2, method = "average") # 평균 거리법
hc_av
plot(hc_av, hang = -1)

par(oma = c(3, 0, 1, 0))
par(mfrow = c(1,3))
plot(hc_sl, hang = -1)
plot(hc_co, hang = -1)
plot(hc_av, hang = -1)

 - 중학생 신체검사 결과

body <- read.csv("testdata/bodycheck.csv")
body
#      번호 악력 신장 체중 안경유무
# 1     1   28  146   34        1
# 2     2   46  169   57        2
# 3     3   39  160   48        2
# 4     4   25  156   38        1
# 5     5   34  161   47        1
# 6     6   29  168   50        1
# 7     7   38  154   54        2
# 8     8   23  153   40        1
# 9     9   42  160   62        2
# 10   10   27  152   39        1
# 11   11   35  155   46        1
# 12   12   39  154   54        2
# 13   13   38  157   57        2
# 14   14   32  162   53        2
# 15   15   25  142   32        1
dim(body)
head(body, 2)

d <- dist(body[, -1]) # 거리계산
d

hc <- hclust(d, method = "complete")
hc
# Cluster method   : complete 
# Distance         : euclidean 
# Number of objects: 15 

plot(hc, hang=-1) # hang=-1 정렬
rect.hclust(hc, k=3, border = "red")

 -  군집별 특징

g1 <- subset(body, 번호 == 10 |번호 == 4 |번호 == 8 |번호 == 1 |번호 == 15)
g2 <- subset(body, 번호 == 11 |번호 == 3 |번호 == 5 |번호 == 6 |번호 == 14)
g3 <- subset(body, 번호 == 2 |번호 == 9 |번호 == 13 |번호 == 7 |번호 == 12)

g1[2:5]
g2[2:5]
g3[2:5]

summary(g1[2:5])
summary(g2[2:5])
summary(g3[2:5])